금척 사용법
금척의 유래와 천부경
해인금척(海印金尺)이란 말은 신화와 전설을 좋아하는 사람이라면 한 번 쯤은 들어보는 이름입니다. 대순전경에도 해인이라는 이름이 나오기 때문에 태을도인들도 은연중에 관심을 가지는 분야이기도 하지요.
해인과 금척이 한 덩어리로 묶여서 전해지는 데에는 그럴만한 이유가 있습니다. 둘이 같은 뿌리에서 출발한 진리의 상징이기 때문이지요. 전에 해인을 설명하면서 금척을 같이 다루려고 했는데, 그 때에는 공사풀이에 전력하던 때라서 금척이라는 재미있는 주제도 뒤로 미룰 수밖에 없었습니다.
이제 천지공사의 중요한 내용은 거의 밝혔기 때문에, 이제 마음의 여유를 가지고 금척이란 어떤 것이며, 어떻게 쓰는 물건인지를 살펴보기로 합니다. 우선 금척에 대한 가장 중요한 전설부터 시작하지요.
대구에서 6번 국도를 타고 남쪽으로 가다가 경주시에 가까와지면 건천읍이 나오고, 조금 더 남쪽으로 내려오면 도로 양쪽에 커다란 무덤들이 모여 있는 모습을 보게 된다. 이곳이 바로 금척(金尺) 고분이라 불리는 신라시대 고분 유적지인데, 이것을 따라 여기 마을 이름도 금척리라고 부른다.

금척은 금으로 만든 자라는 뜻인데, 이 말이 나온 것은 이 고분의 어딘가에 금척이 묻혀져 있다는 설화에 따른 것이다. 금척은 신라 시조왕 박혁거세가 소유했던 통치의 중요한 수단으로, 죽은 사람도 살릴만큼 신묘한 효능을 가진 만병통치의 신물(神物)이었다고 한다.
그 후 당나라가 이 소문을 듣고 탐을 내어 강제로 뺏아 가려 하자 무덤을 만들어 금척을 묻어버리고, 못 찾게 위장하려 수십 개의 무덤도 함께 만드는 바람에 고분군이 조성되었다고 한다. 이 이야기는 금척 고분을 둘러싸고 전해오는 대표적인 전설인데 역사적 사실 진위는 확인하기 어렵고, 실제로는 이 지역에 살았던 신라 호족들의 공동 묘지 같은 것으로 유추하고 있다.
[출처] 신묘한 금척이 묻혀 있다는 경주 금척 고분|작성자 적선인
http://blog.naver.com/rma2443/221226412157
이 전설에 금척을 찾아가는 힌트는 거의 다 들어 있습니다. 가장 중요한 힌트는 박혁거세와 관련되는 신물이라는 점입니다. 그 다음 열쇠는 무덤과 관련된 물건이고, 세 번째 힌트는 병을 고치는 용도로 쓰이는 물건이라는 점이지요.
박혁거세는 신라의 시조로 알려져 있지만 사실은 인류의 시조입니다. ‘성사(聖師) 의통(醫統) 경주(慶州) 용담(龍潭)’의 여덟 글자가 사실은 이 박혁거세를 가리키지요. 왜냐하면 박혁거세(朴赫居世)가 복희(卜羲)씨가 세상(世)에 산다(居)는 뜻을 나타내는 이름이기 때문입니다.
박혁(朴赫)은 큰(朴) 밝음(赫)입니다. 태양신을 가리키며, 태양신 복희와 뜻은 물론이고 발음까지도 비슷합니다. 무엇보다도 확실한 근거는 박혁거세의 죽음과 관련된 기록입니다. 그것도 정사인 삼국사기에 나오는 기록이지요.
“박혁거세가 나라를 다스린 지 61년. 어느 날 하늘로 올라갔는데, 8일 후에 몸뚱이가 땅에 흩어져 떨어졌다. 그리고 왕후 역시 왕을 따라 세상을 하직한다. 나라 사람들이 이들을 합장하여 장사 지내려 했으나, 큰 뱀이 나타나 방해하므로 머리와 사지를 제각기 장사지내 오릉을 만들고 능의 이름을 사릉(巳陵)이라고 하였다. 혹은 뱀이 무덤을 지키기에 사릉이라고 한다.”
위 기록은 삼국사기 박혁거세왕의 죽음에 관한 글이다.
나라의 건국자의 죽음치고는 너무나 처참한 죽음이다...... 이 죽음을 어떻게 받아드려야 하는가? 전형적인 능지처참과 부관참시를 한 번에 행한 모습이다. 건국자이자 시조로 존경받는, 낙랑에서 찬송했고 덕으로 마한을 병합하지 않았고, 변한을 통합한 박혁거세의 죽음이 이렇게 끝났다는 것도 황당하지만, 이러한 박혁거세의 죽음이 널리 알려지지 않음도 이상하다.
출처; 박혁거세의 죽음
여기서 사릉(蛇陵)이라는 이름은 뱀과 관련됩니다. 태호 복희씨의 형상이 뱀이었다고 하니, 그대로 박혁거세와 연결됩니다. 따라서 이 전설은 태호 복희씨의 나라가 여섯으로 쪼개졌음을 후손에게 신화와 전설로 알린 것인데, 이 기록을 역사적 사건으로 보면 능지처참과 부관참시라는 끔찍한 사건으로 해석되지요.
그런데 실제로 상고시대에 이런 일이 있었습니다. 수메르 신화에 기록된 마르두크의 만행이 그 어머니 티아마트를 죽이고 시체를 갈갈이 찢은 것이지요. 이 신화 또한 동이족 한겨레의 신전이 파괴된 과정을 암시하는 기록임은 이미 밝힌 바 있습니다.
거세(居世)의 정확한 뜻은 세 개의 십자가를 상징하는 삼십(三十)을 모시는 신전을 나타내는 이름입니다. 거(居)는 신전이나 교회를 뜻하는 고(古)와 무덤에 모셔진 주검을 나타내는 시(尸)를 합친 글자인데, 주검은 장사를 지낸 다음에는 신상으로 대체되었다가 후일 위패로 바뀌게 되지요. 피라미드에 모셔진 태양신과 태음신과 태일신이 박혁거세의 옳은 뜻입니다.
따라서 경주 오릉은 박혁거세의 무덤이 아닙니다. 박혁거세의 무덤은 이집트의 피라미드이지요. 이 사실은 바로 앞에 올린 글 ‘단군신화의 쑥과 마늘’에서 소개했던 링크 (이시스와 오시리스)에서 피라미드에 모셔진 뱀신들을 보면 알 수 있습니다. 오릉은 피라미드의 배치 방식을 재현하여 근본을 상기시킨 것입니다.

박혁거세의 다음 임금인 남해(南海) 차차웅(次次雄)은 ‘남쪽 바다를 거듭하여 일으켰다’라는 뜻으로도 풀이됩니다. 남(南)은 태양이 가장 높이 솟은 방위입니다. 바다가 어머니의 신전이라는 사실은 더 설명할 필요가 없겠고, 차차웅은 ‘다음다음 숫’으로 읽으면 ‘솟터를 계속하여 일으킨다’는 뜻이 되지요. 그 기간은 무려 일만 년으로 볼 수 있습니다.
결국 스키타이 족의 탈해왕에 이르러서야 신라역사는 오늘날의 한민족과 혈통적으로 연결되는 셈입니다. 그 이전의 역사는 신라 역시 단군의 후예임을 자랑하기 위해서 최초의 조상을 강조하는 기록이 되는 셈이지요.
이런 역사관을 전제로 금척의 비밀을 풀어야 하는 이유는 금척이 피라미드를 만드는 도구이기 때문입니다. 지금부터 그 내용을 밝혀 나가는데, 피라미드와 관계되면서 황금자와 결부되는 것은 아무래도 황금비율이 될 것입니다.
<금척지>에 대한 김시습의 글이 매우 중요한 것은, 지금까지 그 정체를 알 수 없었던 금척의 내용, 형태, 소재 등을 자세히 설명하고 있기 대문이다. 특히 금척은 천부경의 이치를 본떠 만들었으며, 천부경을 영원히 보존하기 위하여 금으로 만들어 보존한 신기(神器)라는 점을 뚜렸이 밝혀 준 점이 중시된다.
“내가 일찍이 <금척지>를 읽으니 그 수사(數辭)가 매우 어려워서 알 수가 없었다. 대저 그 근본은 곧 천부의 법이다. 그것을 금으로 만든 것은 변하지 않게 하기 위한 것이요. 자로 제작한 것은 다 같이 오류가 없게 하기 위함이었다.”
'금척지수리(金尺之數理) 기수사심난(其數辭甚難)'이란 표현으로 보아 금척은 수리(數理)를 세겨 놓은 것임을 알 수 있다. '기본은 천부지법이제지(天符之法而製之)'라는 표현으로 보아 천부경의 법을 본떠 만든 것이며, 수리는 곧 천부경의 수리(數理)임을 알 수 있다.
금척의 생김새를 "그 형상은 삼태성이 늘어선 것 같으니 머리에는 불구슬을 물고 네 마디로 된 다섯 치이다(其形象則如三台之列(기형상칙여삼태지열)하니 頭含火珠(두함화주)하고 四節而五寸(사절이오촌)."라고 설명하고 "그 허실의 수가 9가 되어 10을 이루니, 이는 천부의 수다(其虛實之數(기허실지수)이 九而成十(구이성십)하니 此則天符之數也(차즉천부지수야)."라고 그 수의 내용을 풀이했다. 이로써 금척이 81자로 되어 있는 천부경에 대한 설명임이 확연하게 드러난 것이다.
신라를 세운 근본이 부도 즉 금척의 법에 있으며, 이것이 단군 시대에서 내려 왔다고 한다. 박혁거세 신화를 보면, 그가 알에서 태어났으며 여섯 촌장이 길러 13세에 왕위에 올랐다는 내용이 있는데, 어떻게 13세의 어린아이가 실질적 권력을 가지고 있는 여섯 촌장에 의해서 한 나라의 지배권을 행사했는지 납득이 되지 않는다.
<금척지>의 내용은 이에 대한 실마리를 제공하고 있다. 박혁거세는 연리지가(硏理之家)이며 왕위의 징표가 되는 금척 곧 천부경을 보유하고 있는 집안의 아들이기 때문에 그리 되었다는 것이다. 즉 천지만물의 이치에 통달한 제천군주(祭天君主)였음을 알 수 있는 것이다.
김시습은 <금척지>라도 남았으니 그 도를 연구하여 복제할 길이 있을 것이며, 그렇지 못할지라도 그 법리를 아는 것만으로도 족하다고 했다. 진리불역지전(眞理不易之詮)이 묻혀버리고 생민시원고사(生民始原古史) 적연무문(寂然無聞)함을 한탄했다.
끝으로 '항차 훈민정음 28자를 <징심록>에서 취본(取本)하였음에야' 라는 기록이 나오는데 훈민정음 창제를 새로운 각도에서 연구할 수 있는 중요한 단서라고 생각된다. 우리 상고사를 바르게 아는데 <금척지>야말로 귀중한 문헌일진대 그 원문을 잃었음이 실로 크게 애석할 뿐이다.
http://blog.naver.com/ldk3113/80022175284
천부경을 풀면 피라미드의 형상이 나온다는 사실이야 더 설명할 필요가 없을 것이니 생략하고, 바로 황금비율에 대해서 샆펴 보기로 하지요. 황금비를 재미있게 설명해 놓은 자료를 하나 소개합니다.
금척은 황금비
황금비는 서양에서 주로 쓰이는 아름다움의 척도입니다. 그러다보니 동양에는 황금비와 같은 미적(美的) 기준이 없는 것으로 알았는데, 아래 자료는 동양에도 황금비 못지않은 아름다움의 기준이 있음을 알려주네요.

당 현종이 한 눈에 빠진 절세미인 양귀비의 얼굴이 가진 금강비는 무엇일까요? 서양에서 아름답다고 여기는 황금비와는 어떤 차이점이 있을까요? 동서양의 미의 수학적 기준 금강비와 황금비에 대해 알아봅시다. (중략)
공통적인 비율이 모두 1: 1.4인데요, 정확하게는 1: √2입니다. 이 비율이 바로 금강비(金剛比)입니다. 금강비는 사람뿐만 아니라 동양의 건축물과 예술품에서도 종종 찾아볼 수 있습니다.

우리나라에서 가장 아름다운 건축물로 인정받는 부석사 무량수전에도 금강비가 담겨있는데요. 무량수전의 밑바닥의 가로와 세로가 금강비를 이루고 지붕과 높이 역시 금강비를 이룹니다. 석굴암은 금강비로 만들어진 대표적인 건축물입니다. 석굴암의 구조를 보면 다양한 금강비가 존재합니다.
현재 일상생활에서 가장 자주 접하는 금강비가 담긴 것은 바로 A4용지입니다. A4용지가 우리 곁에 자리 잡게 된 데는 경제학의 원리와 수학적 비밀이 숨어있습니다. 1922년 독일공업규격위원회에서는 큰 종이를 잘라 작은 종이를 만드는 과정에서, 종이의 낭비를 최소화할 수 있는 종이를 도입했는데요. 그 종이의 비율이 바로 금강비를 이룹니다. (중략)
금강비는 중국뿐만 아니라 우리나라와 일본 등 동양에서 아름다운 비율로 여겼습니다. 당 현종은 금강비로 이루어진 양귀비의 얼굴을 절세미인으로 바라봤을 것입니다.
이번에는 서양에서 아름답게 여겨진 황금비(Golden ratio)에 대해 알아봅시다. 요즘 미인의 비율은 ‘1: 1.6’, 정확하게는 ‘1: Ø’입니다. 황금비를 나타내는 기호 Ø는 ‘1: Ø = Ø : 1+Ø’를 만족하는 수입니다.
비례식을 풀어주면 ز = 1 + Ø, ز - Ø - 1 = 0.
근의 공식을 이용하여 Ø의 값을 구하면
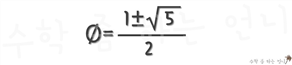
이 두 해 중에서 양의 해를 선택하면, 약 1: 1.618이 됩니다
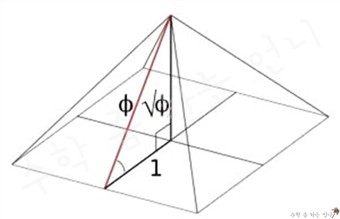
황금비의 역사 또한 매우 긴데요. 무려 기원전 4700년경 기자의 피라미드를 건설하는 데
황금비를 신성한 비율로 사용했습니다. 피라미드의 밑면의 중심에서 밑면의 모서리까지와, 밑면의 모서리에서 피라미드의 꼭대기까지의 비율이 거의 정확하게 황금비를 이룹니다.
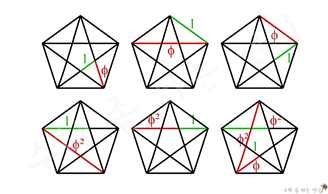
피타고라스학파는 황금비를 이용하여 정오각형 안에 별을 그렸는데, 모서리와 대각선이 황금비를 이루고, 각 꼭짓점을 잇는 선분들이 다양한 형태로 황금비를 이룹니다.
동양에서 아름답다고 여긴 금강비와 서양에서 아름답다고 여긴 황금비는 조금의 차이는 있지만, 수학적으로 무리수에 해당하는 두 비율이 오랜 역사를 가지고 있다는 것은 놀랄만한 사실입니다 .
[출처] [황금비와 금강비] |작성자 임티처
http://blog.naver.com/attractorlim/221382505817
외국 영화를 보면서는 영상이 멋있다거나 등장인물들이 예쁘다는 생각은 들지만, 아름답고 사랑스럽다는 생각은 들지 않았던 이유를 금강비를 알고서야 이해했습니다. 동양인과 서양인의 두뇌구조 자체가 음양의 법칙에 따라 차이가 있기 때문에 아름다움에 대한 느낌이 다를 수밖에 없었던 것이지요.
그렇다고 두 아름다움 사이에 우열이 있는 것이 아닙니다. 아름다움이란 자연에 내재한 존재와 변화의 법칙으로서 패턴이라고 말할 수 있는 것이고, 그 패턴에 가까울수록 아름답게 느껴지고, 멀어지면 추하게 인식됩니다. 그러므로 아름다움은 우주질서의 흐름 속에 사는 사람에게는 거역할 수 없는 매력으로 다가옵니다.
그래서 아름다움은 힘이 되지요. 인류의 문화는 이 아름다움을 찾아내고 모방하며 실현시키는 활동의 역사입니다. 그리고 풍류는 가장 오랫동안 실생활의 모든 분야에서 그 아름다움을 찾아온 심미(審美) 문화의 주류이지요. 그래서 음악, 미술, 건축, 공예. 요리, 놀이 등 문화예술 전반에서 최고 수준의 경지를 자랑하지요.
아무튼 금강비와 황금비는 서로 다른 두 측면의 아름다움입니다. 황금비는 발산하는 양성적 아름다움이고, 금강비는 수렴하는 음성적 아름다움이지요. ‘1 ; 1.5’가 중정미(中正美)라고 할 수 있는데, 이 아름다움은 절대적인 아름다움이지만 확산이나 수렴의 운동변화에 편승하고 있는 인간의 상황에서는 아름답다고 느끼기 힘들지요.
그래서 중정미에서 ‘0.1’의 비례치가 차이 나는 음성적 금강비나 양성적 황금비가 사람의 기호를 결정하게 된다고 보면 됩니다. 황금비와 금강비가 무리수로 나타나는 것은 개개인의 물리적, 심리적 사회문화적 상황의 편차를 반영할 수 있는 여지를 주는 것이겠네요.
아무튼 아름다움이란 중성의 발현이라고 정의할 수 있습니다. 음과 양의 균형과 조화를 많이 반영하는 모습이 아름다움의 본질이라는 것이지요. 박용숙 선생이 꽃이 풍류의 상징이 된 이유를 천부경의 중성이 발현되는 부풀음에서 찾은 것은 정말 뛰어난 통찰이지요.
육(六)과 음양오행
천부경의 중앙수 육(六)은 위 그림의 오른쪽 그림처럼 부풀어나는 모습으로 이해되기도 합니다. 그 진리를 처음 소개한 사람이 박용숙 선생이지요. 음양오행의 원리 설명은 해당 자료를 소개하는 것으로 대신하려 합니다. (꽃의 비의와 인체 http://blog.naver.com/ilkong36/221372436770)

석가모니의 염화미소의 도구였던 연꽃이 개화하는 모습입니다. 블로그로 들어가 보시면 타임랩스 동영상으로 구경하실 수 있지요. 그리고 샤로트 사전의 도상학 기호로 풀이했다는 마지막 단계인 회전현상을 수학에서는 피보나치수열이라고 부르고, 다른 이름으로 황금비례라고도 하는데 내친 김에 해당 자료도 얻어 왔습니다.
출처; 졸작 천부경 쉬운 풀이 7 - 육과 음양오행
부풀음이 아름다움이 되는 이유는 차원의 상승과 관계가 있습니다. 잎이 이차원 평면의 성장방식을 보이는 반면, 꽃은 솟구쳐서 옆으로 벌어지는 입체적인 성장형식이고, 그 내부에는 나선형 꽃잎배열 방식으로 회전운동까지 담고 있지요. 이것을 천부경에서는 ‘육생칠팔구운(六生七八九運)이라고 표현하고, 테슬라의 369 코드에서는 369는 다른 124, 578과는 차원이 다르다고 설명합니다.
댓글 올리신 분이 문의하신 내용의 답글에 올린 그림이 너무 작게 보여서 여기에 추가합니다.
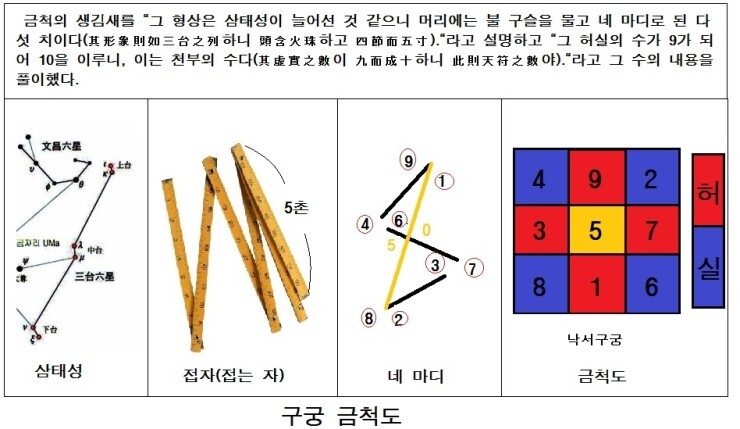
[출처] 금척 사용법 1 - 금척의 유래와 천부경|작성자 구름따라
'신성 Holy > 기하학 형태' 카테고리의 다른 글
| 금척 사용법 3 - 카발라와 천문성좌 (0) | 2022.01.11 |
|---|---|
| 금척 사용법 2 - 금척과 황금비 (0) | 2022.01.11 |
| 케네스 스넬슨의 텐세그리티 (0) | 2021.06.28 |
| thrive 다큐 (0) | 2021.05.27 |
| 신성기하학 십계명(댄 윈터) (0) | 2021.05.06 |